The International Temperature Scale of 1990
The International Temperature Scale of 1990 was adopted by the International Committee of Weights and Measures at its meeting in 1989, in accordance with the request embodied in Resolution 7 of the 18th General Conference of Weights and Measures of 1987. This scale supersedes the International Practical Temperature Scale of 1968 (amended edition of 1975) and the 1976 Provisional 0.5 K to 30 K Temperature Scale.
1. Units of Temperature
The unit of the fundamental physical quantity known as thermodynamic temperature, symbol T, is the kelvin symbol K, defined as the fraction 1/273.16 of the thermodynamic temperature of the triple point of water1.
Because of the way earlier temperature scales were defined, it remains common practice to express a temperature in terms of its difference from 273.15 K, the ice point. A thermodynamic temperature, T, expressed in this way is known as a Celsius temperature, symbol t, defined by:
t / ºC = T / K - 273.15 (1)
The unit of Celsius temperature is the degree Celsius, symbol ºC, which is by definition equal in magnitude to the kelvin. A difference of temperature may be expressed in kelvins or degrees Celsius.
The International Temperature Scale of 1990 (ITS-90) defines both International Kelvin Temperatures, symbol T90, and International Celsius Temperatures, symbol T90. The relation between T90 and T90 is the same as that between T and t, i.e.:
t90 / ºC = T90 / K - 273.15 (2)
The unit of the physical quantity T90 is the kelvin, symbol K, and the unit of the physical quantity T90 is the degree Celsius, symbol ºC, as is the case for the thermodynamic temperature T and the Celsius temperature t.
2. Principles of the International Temperature Scale of 1990 (ITS-90)
The ITS-90 extends upwards from 0.65 K to the highest temperature practicably measurable in terms of the Planck radiation law using monochromatic radiation. The ITS-90 comprises a number of ranges and sub-ranges throughout each of which temperatures T90 are defined. Several of these ranges or sub-ranges overlap, and where such overlapping occurs, differing definitions of T90 exist: these differing definitions have equal status. For measurements of the very highest precision there may be detectable numerical differences between measurements made at the same temperature but in accordance with differing definitions. Similarly, even using one definition, at a temperature between defining fixed points two acceptable interpolating instruments (e.g. resistance thermometers) may give detectably differing numerical values of T90. In virtually all cases these differences are of negligible practical importance and are at the minimum level consistent with a scale of no more than reasonable complexity; for further information on this point see "Supplementary information for the ITS-90" (BIPM-1990).
The ITS-90 has been constructed in such a way that, throughout its range, any given temperature the numerical value of T90 is a close approximation to the numerical value of T90 according to best estimates at the time the scale was adopted. By comparison with direct measurements of thermodynamic temperatures, measurements of T90 are more easily made, are more precise and are highly reproducible.
There are significant numerical differences between the values of T90 and the corresponding values of T90 measured on the International Practical Temperature Scale of 1968 (IPTS-68), see Fig. 1 and Table 6. Similarly there were differences between the IPTS-68 and the International Practical Temperature Scale of 1948 (IPTS-48), and between the International Temperature Scale of 1948 (ITS-48) and the International Temperature Scale of 1927 (ITS-27). See the Appendix, and, for more detailed information, "Supplementary Information for the ITS-90."
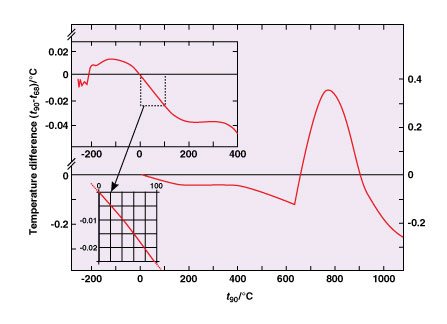
FIG. 1. The differences (t90 - t68) as a function of Celsius temperature t90.
3. Definition of the International Temperature Scale of 1990
Between 0.65 K and 5.0 K T90 is defined in terms of the vapour-pressure temperature relations 3He and 4He.
Between 3.0 K and the triple point of neon (24.5561 K) T90 is defined by means of a helium gas thermometer calibrated at three experimentally realizable temperatures having assigned numerical values (defining fixed points) and using specified interpolation procedures.
Between the triple point of equilibrium hydrogen (13.8033 K) and the freezing point of silver (961.78 ºC) T90 is defined by means of platinum resistance thermometers calibrated at specified sets of defining fixed points and using specified interpolation procedures.
Above the freezing point of silver (961.78ºC) T90 is defined in terms of a defining fixed point and the Planck radiation law.
The defining fixed points of the ITS-90 are listed in Table 1. The effects of pressure, arising from significant depths of immersion of the sensor or from other causes, on the temperature of most of these points are given in Table 2.
3.1. From 0,65 K: Helium Vapour-Pressure Temperature Equations
In this range T90 is defined in terms of the vapour pressure p of 3He and 4He using equations of the form:
9
T90/K = Ao+∑Ai[(in (p/Pa) —B)/C)i
i=1
The values of the constants A0, Ai, B and C are given in Table 3 for 3He in the range of
0.65 K to 3.2 K, and for 4He in the ranges 1.25 K to 2.1768 K (the lambda point) and 2.1768 K to 5.0 K.
3.2 From 3.0 K to the Triple Point of Neon (24.5561 K): Gas Thermometer
In this range T90 is defined in terms of a 3He or a 4He gas thermometer of the constant-volume type that has been calibrated at three temperatures. These are the triple point of neon (24.5561 K), the triple point of equilibrium hydrogen (13.8033 K), and a temperature is between 3.0 K and 5.0 K. This last temperature is determined using a 3He or a 4He vapour pressure thermometer as specified in Sect. 3.1.
Table 1. Defining fixed points of the ITS-90
| Temperature | |||||
|---|---|---|---|---|---|
| Number | T90/K | t90/ºC | Substancea | Stateb | Wr(T90) |
| 1 | 3 to 5 | -270.15 to -268.15 |
He | V | |
| 2 | 13.8033 | -259.3467 | e-H2 | T | 0.001 190 07 |
| 3 | ~17 | ~-256.15 | e-H2 (or He) |
V (or G) |
|
| 4 | ~20.3 | ~-252.85 | e-H2 (or He) |
V (or G) |
|
| 5 | 24.5561 | -248.5939 | Ne | T | 0.008 449 74 |
| 6 | 54.3584 | -218.7916 | O2 | T | 0.091 718 04 |
| 7 | 83.8058 | -189.3442 | Ar | T | 0.215 859 75 |
| 8 | 234.3156 | -38.8344 | Hg | T | 0.844 142 11 |
| 9 | 273.16 | 0.01 | H2O | T | 1.000 000 00 |
| 10 | 302.9146 | 29.7646 | Ga | M | 1.118 138 89 |
| 11 | 429.7485 | 156.5985 | In | F | 1.609 801 85 |
| 12 | 505.078 | 231.928 | Sn | F | 1.892 797 68 |
| 13 | 692.677 | 419.527 | Zn | F | 2.568 917 30 |
| 14 | 933.473 | 660.323 | Al | F | 3.376 008 60 |
| 15 | 1234.93 | 961.78 | Ag | F | 4.286 420 53 |
| 16 | 1337.33 | 1064.18 | Au | F | |
| 17 | 1357.77 | 1084.62 | Cu | F | |
(a) All substances except 3He are of natural isotopic composition, e-H2 is hydrogen at the equilibrium concentration of the ortho- and para-molecular forms
(b) For complete definitions and advice on the realization of these various states, see "Supplementary Information for the ITS-90". The symbols have the following meanings: V: vapour pressure point; T: triple point (temperature at which the solid liquid and vapour phases are in equilibrium); G: gas thermometer point; M, F: melting point, freezing point (temperature, at a pressure of 101 325 Pa, at which the solid and liquid phases are in equilibrium)
Table 2. Effect of pressure on the temperatures of some defining fixed points+
| Substance | Assignment value of equilibrium temperature T90/K |
Temperature with pressure, p (dT/dp)/ (10-8K · Pa -1)* |
Variation with depth, lambda (dT/dl)/ (10-3K · m -1)** |
|---|---|---|---|
| e-Hydrogen (T) | 13.8033 | 34 | 0.25 |
| Neon (T) | 24.5561 | 16 | 1.9 |
| Oxygen (T) | 54.3584 | 12 | 1.5 |
| Argon (T) | 83.8058 | 25 | 3.3 |
| Mercury (T) | 234.3156 | 5.4 | 7.1 |
| Water (T) | 273.16 | - 7.5 | - 0.73 |
| Gallium | 302.9146 | - 2.0 | - 1.2 |
| Indium | 429.7485 | 4.9 | 3.3 |
| Tin | 505.078 | 3.3 | 2.2 |
| Zinc | 692.677 | 4.3 | 2.7 |
| Aluminium | 933.473 | 7.0 | 1.6 |
| Silver | 1234.93 | 6.0 | 5.4 |
| Gold | 1337.33 | 6.1 | 10 |
| Copper | 1357.77 | 3.3 | 2.6 |
* Equivalent to millikelvins per standard atmosphere
** Equivalent to millikelvins per metre of liquid
+ The Reference pressure for melting and freezing points is the standard atmosphere (p0=101 325 Pa). For triple points (T) the pressure effect is a consequence only of the hydrostatic head of liquid in the cell
Table 3. Values of the constants for the helium vapour pressure Eqs. (3), and the temperature range for which each equation, identified by its set of constants, is valid
| 3He 0.65 K to 3.2 K |
4He 1.25 K to 2.1768 K |
4He 2.1768 K to 5.0 K |
|
|---|---|---|---|
| A0 | 1.053 447 | 1.392 408 | 3.146 631 |
| A1 | 0.980 106 | 0.527 153 | 1.357 655 |
| A2 | 0.676 380 | 0.166 756 | 0.413 923 |
| A3 | 0.372 692 | 0.050 988 | 0.091 159 |
| A4 | 0.151 656 | 0.026 514 | 0.016 349 |
| A5 | - 0.002 263 | 0.001 975 | 0.001 826 |
| A6 | 0.006 596 | - 0.017 976 | - 0.00 4325 |
| A7 | 0.088 966 | 0.005 409 | - 0.00 4973 |
| A8 | - 0.004 770 | 0.013 259 | 0 |
| A9 | - 0.054 943 | 0 | 0 |
| B | 7.3 | 5.6 | 10.3 |
| C | 4.3 | 2.9 | 1.9 |
3.2.1. From 4.2 K to the Triple Point of Neon (24.5561 K) with 4He as the Thermometric Gas.
In this range T90 is defined by the relation:
T90 = a + bp +cp2, (4)
where p is the pressure in the gas thermometer and a, b and c are coefficients the numerical values of which are obtained from measurements made at the three defining fixed points given in Sect. 3.2. but with the further restriction that the lowest one of these points lies between 4.2 K and 5.0 K.
3.2.2. From 3.0 K to the Triple Point of Neon (24.5561 K) with 3He or 4He as the Thermometric Gas.
For a 3He gas thermometer, and for a 4He gas thermometer used below 4.2 K, the non-ideality of the gas must be accounted for explicitly, using the appropriate second virial coefficient B3 (T90) or B4 (T90). In this range T90 is defined by the relation:
T90 = a + bp + cp2/1 + Bx(T90) NIV
where p is the pressure in the gas thermometer, a, b and c are coefficients the numerical values of which are obtained from measurements at three defining temperatures as given in Sect. 3.2, N/V is the gas density with N being the quantity of gas and V the volume of the bulb, X is 3 or 4 according to the isotope used, and the values of the second virial coefficients are given by the relations:
B(T90)/m3mol-1={16,69 — 336,98(T90/K)-1
+91,04(T90/K)-2—13,82(T90/K)-3} 10-6
For 4He
B4(T90)/m3mol-1={15,708—374,05(T90/K)-1
—383,53(T90/K)-2-2 + 1799,2(T90/K)-3
—4033,2(T90/K)-4 + 3252,8 (T90/K)-3} 10-6
Table 4. The constants A0, Ai; Bn, Bi; C0, Ci; D0 and Di in the reference functions of equations (9a); (10a); and (10b) respectively
| A0 | - 2.135 347 29 | B0 | 0.183 324 722 | C0 | 2.781 572 54 | D0 | 439.932 854 |
| A1 | 3.183 247 20 | B1 | 0.240 975 303 | C1 | 1.646 509 16 | D1 | 472.418 020 |
| A2 | - 1.801 435 97 | B2 | 0.209 108 771 | C2 | - 0.137 143 90 | D2 | 37.684 494 |
| A3 | 0.717 272 04 | B3 | 0.190 439 972 | C3 | - 0.006 497 67 | D3 | 7.472 018 |
| A4 | 0.503 440 27 | B4 | 0.142 648 498 | C4 | - 0.002 344 44 | D4 | 2.920 828 |
| A5 | - 0.618 993 95 | B5 | 0.077 993 465 | C5 | 0.005 118 68 | D5 | 0.005 184 |
| A6 | - 0.053 323 22 | B6 | 0.012 475 611 | C6 | 0.001 879 82 | D6 | - 0.963 864 |
| A7 | 0.280 213 62 | B7 | - 0.032 267 127 | C7 | - 0.002 044 72 | D7 | - 0.188 732 |
| A8 | 0.107 152 24 | B8 | - 0.075 291 522 | C8 | - 0.000 461 22 | D8 | 0.191 203 |
| A9 | - 0.293 028 65 | B9 | - 0.056 470 670 | C9 | 0.000 457 24 | D9 | 0.049 025 |
| A10 | 0.044 598 72 | B10 | 0.076 201 285 | ||||
| A11 | 0.118 686 32 | B11 | - 0.123 893 204 | ||||
| A12 | - 0.052 481 34 | B12 | - 0.029 201 193 | ||||
| B13 | - 0.091 173 542 | ||||||
| B14 | 0.001 317 696 | ||||||
| B15 | 0.026 025 526 |
The accuracy with which T90 can be realized using Eqs. (4) and (5) depends on the design of the gas thermometer and the gas density used. Design criteria and current good practice required to achieve a selected accuracy are given in "Supplementary Information for the ITS -90".
3.3. The Triple Point of Equilibrium Hydrogen (13.8033 K) to the Freezing Point of Silver (961.78 ºC): Platinum Resistance Thermometer
In this range T90 is defined by means of a platinum resistance thermometer calibrated at specified sets of defining fixed points, and using specified reference and deviation functions for interpolation at intervening temperatures.
No single platinum resistance thermometer can provide high accuracy, or is even likely to be usable, over all of the temperature range 13,8033 K to 961.78 ºC. The choice of temperature range, or ranges, from among those listed below for which a particular thermometer can be used is normally limited by its construction.
For practical details and current good practice, in particular concerning types of thermometer available, their acceptable operating ranges, probable accuracies, permissible leakage resistance, resistance values, and thermal treatment, see "Supplementary Information for ITS-90". It is particularly important to take account of the appropriate heat treatments that should be followed each time a platinum resistance thermometer is subjected to a temperature above about 420 ºC.
Temperatures are determined in terms of the ratio of the resistance R(T90) at a temperature T90 and the resistance R (273.16 K) at the triple point of water.
This ratio, W (T90), is 2:
W(T90)=R(T90)/IR(273,16K)
2 Note that this definition of W (T90) differs from the corresponding definition used in the ITS-27, ITS-48, IPTS-48, and IPTS-68: for all of these earlier scales W (T) was defined in terms of reference temperature of 0ºC, which since 1954 has itself been defined as 273.15 K
An acceptable platinum resistance thermometer must be made from pure, strain-free platinum, and it must satisfy at least one of the following two relations:
W(27,7646°C)=1,118,07
W)—38,8344°C)=0,844 235
An acceptable platinum resistance thermometer that is to be used up to the freezing point of silver must also satisfy the relation:
W(961,78°C)=4,2844
In each of the resistance thermometer ranges, T90 is obtained from W (T90) as given by the appropriate reference function {Eqs. (9b) or (10b)}, and the deviation W(T90) - Wr(T90). At the defining fixed points this deviation is obtained directly from the calibration of the thermometer: at intermediate temperatures it is obtained by means of the appropriate deviation function {Eqs. (12), (13) and (14)}.
(i) - For the range 13.8033 K to 273.16 K the following reference function is defined:
12
(9a.)In [Wr(T90)]=A0 + ?Ai[In (T90)/273,16K + 1,5/1,5]i
i=1
An inverse fnction, equivalent to Eq.(9a.) to within 0,1 mK, is:
15
(9b.) T90/273,16K = B0 + ? Bi[Wr(T90)1/6 —0,65/0,35]i
i=1
The values of the constants A0, Ai, B0 and Bi are given in Table 4.
A thermometer may be calibrated for use throughout this range or, using progressively fewer calibration points, for ranges with low temperature limits of 24.5561 K, 54.3584 K and 83.8058 K, all having an upper limit of 273.16 K.
(ii) - For the range 0 ºC to 961.78 ºC the following reference function is defined:
9
(10a.) Wr(T90) = C0 + ?Ci[T90/K — 754,15/481]i
i=1
An inverse function, equivalent to equation (10a.) to within 0,13 mK is:
9
(10b.) T90/K — 273,15 = D0 + ? Di[Wr(T90) — 2,64/1,64]i
i=1
The values of the constants C0, Ci, D0 and Di are given in Table 4.
A thermometer may be calibrated for use throughout this range or, using fewer calibration points, for ranges with upper limits of 660.323 ºC, 419.527 ºC, 231.928 ºC, 156.5985 ºC or 29.7646 ºC, all having a lower limit of 0 ºC.
(iii) - A thermometer may be calibrated for use in the range 234.3156 K ( - 38.8344 ºC) to 29.7646 ºC, the calibration being made at these temperatures and at the triple point of water. Both reference functions {Eqs. (9) and (10)} are required to cover this range.
The defining fixed points and deviation functions for the various ranges are given below, and in summary from in Table 5.
3.3.1. The Triple Point of Equilibrium Hydrogen (13.8033 K) to the Triple Point of Water (273.16 K).
The thermometer is calibrated at the triple points of equilibrium hydrogen (13.8033 K), neon (24.5561 K), oxygen (54.3584 K), argon (83.8058 K), mercury (234.3156 K), and water (273.16 K), and at two additional temperatures close to 17.0 K and 20.3 K. These last two may be determined either: by using a gas thermometer as described in Sect. 3.2, in which case the two temperatures must lie within the ranges 16.9 K to 17.1 K and 20.2 K to 20.4 K respectively; or by using the vapour pressure-temperature relation of equilibrium hydrogen, in which case the tow temperatures must lie within the ranges 17.025 K to 17.045 K and 20.26 K to 20.28 K respectively, with the precise values being determined from Eqs. (11a) and (11b) respectively:
T90/K - 17.035 = (p/kPa - 33.3213)/13.32 (11a)
T90/K - 20.27 = (p/kPa - 101.292)/30 (11b)
(11a.) T90/K — 17,035 = (p/kPa — 33,3213)/13,32
(11b.) T90/K — 20,27 = (p/kPa — 101,292)/30
The deviation function is3
5
(12.) W(T90) — Wr(T90) = a[W(T90)—1] + b[W(T90)—]2 + ? ci[In W(T90)]i+n
i=1
3 This deviation function {and also those of Eqs. (13) and (14)} may be expressed in terms of Wr rather than W; for this procedure see "Supplementary Information for ITS-90"
with values for the coefficients a, b and ci being obtained from measurements at the defining fixed points and with n = 2.
For this range and for the sub-ranges 3.3.1.1 to 3.3.1.3 the required values Wr(T90) are obtained from Eq. (9a) or from Table 1.
3.3.1.1. The Triple Point of Neon (24.5561 K) to the Triple Point of Water (273.16 K).
The thermometer is calibrated at the triple points of equilibrium hydrogen (13.8033 K), neon (24.5561 K), oxygen (54.3584 K), argon (83.8058 K), mercury (234.3156 K) and water (273.16 K).
The deviation function is given by Eq. (12) with values for the coefficients a, b, c1, c2 and c3 being obtained from measurements at the defining fixed points and with c4 = c5 = n = 0.
3.3.1.2 The Triple Point of Oxygen (54.3584 K) to the Triple Point of Water (273.16 K).
The thermometer is calibrated at the triple points of oxygen (54.3584 K), argon (83.8058 K), mercury (234.3156 K) and water (273.16 K).
Table 5. Deviation functions and calibration points for platinum resistance thermometers in the various ranges in which they define T90
| a. Ranges with an upper limit of 273.16 K | |||
| Section | Lower temperature limit (T/K) |
Deviation functions | Calibration points (see Table 1) |
|---|---|---|---|
| 3.3.1 | 13.8033 | As equation (12), with n=2 | 2-9 |
| 3.3.1.1 | 24.5561 | As for 3.3.1 with c4 = c5 = n = 0 | 2, 5-9 |
| 3.3.1.2 | 54.3584 | As for 3.3.1 with c2 = c3 = c4 = c5 = 0, n = 1 | 6-9 |
| 3.3.1.3 | 83.8058 | a[W (T90) - 1]+b[W (T90) - 1] ln W (T90) | 7-9 |
| b. Ranges with a lower limit of 0 ºC | |||
| Section | Lower temperature limit (t/ºC) |
Deviation functions | Calibration points (see Table 1) |
| 3.3.2* | 961.78 | As equation (14) | 9, 12-15 |
| 3.3.2.1 | 660.323 | As for 3.3.2 with d = 0 | 9, 12 - 14 |
| 3.3.2.2 | 419.527 | As for 3.3.2 with c = d = 0 | 9, 12, 13 |
| 3.3.2.3 | 231.928 | As for 3.3.2 with c = d = 0 | 9, 11, 12 |
| 3.3.2.4 | 156.5982 | As for 3.3.2 with b = c = d = 0 | 9, 11 |
| 3.3.2.5 | 29.7646 | As for 3.3.2 with b = c = d = 0 | 9, 10 |
| c. Range from 234.3156 K ( - 38.8344 ºC) to 29.7646 ºC | |||
| 3.3.3 | As for 3.3.2 with c = d = 0 | 8-10 |
* Calibration points 9, 12-14 are used with d = 0 for t90 <= 660.323 ºC; the values of a, b and c thus obtained are retained for t90 => 660.323 ºC with d being determined from calibration point 15
The deviation function is given by Eq. (12) with values for the coefficients a, b and c1 being obtained from measurements at the defining fixed points, with c2 = c3 = c4 = c5 = 0 and with n = 1.
3.3.1.3. The Triple Point of Argon (83.8058 K) to the Triple Point of Water (273.16 K).
The thermometer is calibrated at the triple points of argon (83,8058 K), mercury (234,3156 K) and water (273,16 K).
The deviation function is:
(13.) W(T90) — Wr(T90) = a[W(T90)—1] + b[W(T90)—1] In W(T90)
with the values of a and b being obtained from measurements at the defining fixed points.
3.3.2. From 0 ºC to the Freezing Point of Silver (961.78 ºC).
The thermometer is calibrated at the triple point of water (0,01 ºC), and at the freezing points of tin (231.928 ºC), zinc (419.527 ºC), aluminium (660.323 ºC) and silver (961.78 ºC).
The deviation function is:
(14.) W(T90) — Wr(T90) = a[W(T90)—1] + b[W(T90)—1]2 + c[W(T90)—1]3 + d[W(T90)—W(660,323 °C)]2
For temperatures below the freezing point of aluminium d = 0, with the values of a, b and c being determined from the measured deviations from Wr(T90) at the freezing points of tin, zinc and aluminium. From the freezing point of aluminium to the freezing point of silver the above values of a, b and c are retained and the value of d is determined from the measured deviation from Wr(T90) at the freezing point of silver.
For this range and for the sub-ranges 3.3.2.1 to 3.3.2.5 the required values for Wr(T90) are obtained from Eq. (10a) or from Table 1.
3.3.2.1. From 0 ºC to the Freezing Point of Aluminium (660.323 ºC).
The thermometer is calibrated at the triple point of water (0.01 ºC), and at the freezing points of tin (231.928 ºC), zinc (419.527 ºC) and aluminium (660.323 ºC).
The deviation function is given by Eq. (14), with the values of a, b and c being determined from measurements at the defining fixed points and with d = 0.
3.3.2.2. From 0 ºC to the Freezing Point of Zinc (419.527 ºC).
The thermometer is calibrated at the triple point of water (0.0 ºC), and at the freezing points of tin (231.928 ºC). and zinc (419.527 ºC).
The deviation function is given by Eq. (14), with the values of a and b being obtained from measurements at the defining fixed points and with c = d = 0.
3.3.2.3. From 0 ºC to the Freezing Point of Tin (231.928 ºC).
The thermometer is calibrated at the triple point of water (0.01 ºC), and at the freezing points of indium (156.5985 ºC) and tin (231.928 ºC).
The deviation function is given by Eq. (14), with the values of a and b being obtained from measurements at the defining fixed points and with c = d = 0.
3.3.2.4.From 0 ºC to the Freezing Point of Indium (156,5985 ºC).
The thermometer is calibrated at the triple point of water (0.01 ºC), and at the freezing point of indium (156.5985 ºC).
The deviation function is given by Eq. (14) with the value of a being obtained from measurements at the defining fixed points and with b = c = d = 0.
3.3.2.5. From 0 ºC to the Melting Point of Gallium (29.7646 ºC).
The thermometer is calibrated at the triple point of water (0.01 ºC), and the melting point of gallium (29.7646 ºC).
The deviation function is given by Eq. (14) with the value of a being obtained from measurements at the defining fixed points and with b = c = d = 0.
3.3.3. The Triple Point of Mercury (-38.8344 ºC) to the Melting Point of Gallium (29.7646 ºC).
The thermometer is calibrated at the triple points of mercury (- 38.8344 ºC), and water (0.01 ºC), and at the melting point of gallium (29.7646 ºC).
The deviation function is given by Eq. (14) with the values of a and b being obtained from measurements at the defining fixed points and with c = d = 0.
The required values of Wr(T90) are obtained from Eqs. (9a) and (10a) for measurements below and above 273.16 K respectively, or from Table 1.
3.4. The Range Above the Freezing Point of Silver (961,78 ºC): Planck Radiation Law
Above the freezing point of silver the temperature T90 is defined by the equation:
(15.) L?(T90)/L?[(T90(X)]=exp(c2[?T90(X)]-1)—1/exp(c2[?T90]-1)—1
where T90(X) refers to any one of the silver {T90(Ag) = 1234.93 K}, the gold {T90(Au) = 1337.33 K} or the copper {T90(Cu) = 1357.77 K} freezing points4 and in which Llambda(T90) and Llambda[T90(X)] are the spectral concentrations of the radiance of a blackbody at the wavelength (in vacuo) lambda at T90 and at T90(X) respectively, and c2 = 0.014388 m · K
. For practical details and current good practice for optical pyrometry, see "Supplementary Information for the ITS-90" (BIPM-1990).
4 The T90 values of the freezing points of silver, gold and copper are believed to be self consistent to such a degree that the substitution of any one of them in place of one of the other two as the reference temperature T90(X) will not result in significant differences in the measured values of T90.
4. Supplementary Information and Differences from Earlier Scales
The apparatus, methods and procedures that will serve to realize the ITS-90 are given in "Supplementary Information for the ITS-90". This document also gives an account of the earlier International Temperature Scales and the numerical differences between successive scales that include, where practicable, mathematical functions for differences T90 - T68. A number of useful approximations to the ITS-90 are given in "Techniques for Approximating the ITS-90".
These two documents have been prepared by the Comité Consultatif de Thermométrie and are published by the BIPM; they are revised and updated periodically. The differences T90 - T68 are shown in Fig. 1 and Table 6. The number of significant figures given in Table 6 allows smooth interpolations to be made.
However, the reproducibility of the IPTS-68 is, in many areas, substantially worse than is implied by this number.
Table 6. Differences between ITS-90 and EPT-76, and between ITS-90 and IPTS-68 for specified values of T90 and t90.
Table 6. Differences between ITS-90 and EPT-76, and between ITS-90 and IPTS-68 for specified values of T90 and t90.
| (T90 - T76)/mK | ||||||||||
| T90/K | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.1 | -0.2 | -0.3 | -0.4 | -0.5 | |||||
| 10 | -0.6 | -0.7 | -0.8 | -1.0 | -1.1 | -1.3 | -1.4 | -1.6 | -1.8 | -2.0 |
| 20</ | -2.2 | -2.5 | -2.7 | -3.0 | -3.2 | -3.5 | -3.8 | -4.1 | ||
| (T90 - T68)/K | ||||||||||
| T90/K | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | -0.006 | -0.003 | -0.004 | -0.006 | -0.008 | -0.009 | ||||
| 20 | -0.009 | -0.008 | -0.007 | -0.007 | -0.006 | -0.005 | -0.004 | -0.004 | -0.005 | -0.006 |
| 30 | -0.006 | -0.007 | -0.008 | -0.008 | -0.008 | -0.007 | -0.007 | -0.007 | -0.006 | -0.006 |
| 40 | -0.006 | -0.006 | -0.006 | -0.006 | -0.006 | -0.007 | -0.007 | -0.007 | -0.006 | -0.006 |
| 50 | -0.006 | -0.005 | -0.004 | -0.004 | -0.003 | -0.002 | -0.001 | 0.000 | 0.001 | 0.002 |
| 60 | 0.003 | 0.003 | 0.004 | 0.004 | 0.005 | 0.005 | 0.006 | 0.006 | 0.007 | 0.007 |
| 70 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 |
| 80 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 |
| 90 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.009 | 0.009 | 0.009 |
| T90/K | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| 100 | 0.009 | 0.011 | 0.013 | 0.014 | 0.014 | 0.014 | 0.014 | 0.013 | 0.012 | 0.012 |
| 200 | 0.011 | 0.010 | 0.009 | 0.008 | 0.007 | 0.005 | 0.003 | 0.001 | ||
| (t90 -t68)/ºC | ||||||||||
| t90/ºC | 0 | -10 | -20 | -30 | -40 | -50 | -60 | -70 | -80 | -90 |
| -100 | 0.013 | 0.013 | 0.014 | 0.014 | 0.014 | 0.013 | 0.012 | 0.010 | 0.008 | 0.008 |
| 0 | 0.000 | 0.002 | 0.004 | 0.006 | 0.008 | 0.009 | 0.010 | 0.011 | 0.012 | 0.012 |
| t90/ºC | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| 0 | 0.000 | -0.002 | -0.005 | -0.007 | -0.010 | -0.013 | -0.016 | -0.018 | -0.021 | -0.024 |
| 100 | -0.026 | -0.028 | -0.030 | -0.032 | -0.034 | -0.036 | -0.037 | -0.038 | -0.039 | -0.039 |
| 200 | -0.040 | -0.040 | -0.040 | -0.040 | -0.040 | -0.040 | -0.040 | -0.039 | -0.039 | -0.039 |
| 300 | -0.039 | -0.039 | -0.039 | -0.040 | -0.040 | -0.041 | -0.042 | -0.043 | -0.045 | -0.046 |
| 400 | -0.048 | -0.051 | -0.053 | -0.056 | -0.059 | -0.062 | -0.065 | -0.068 | -0.072 | -0.075 |
| 500 | -0.079 | -0.083 | -0.087 | -0.090 | -0.094 | -0.098 | -0.101 | -0.105 | -0.108 | -0.112 |
| 600 | -0.115 | -0.118 | -0.122 | - 0.125* | -0.08 | -0.03 | 0.02 | 0.06 | 0.11 | 0.16 |
| 700 | 0.20 | 0.24 | 0.28 | 0.31 | 0.33 | 0.35 | 0.36 | 0.36 | 0.36 | 0.35 |
| 800 | 0.34 | 0.32 | 0.29 | 0.25 | 0.22 | 0.18 | 0.14 | 0.10 | 0.06 | 0.03 |
| 900 | -0.01 | -0.03 | -0.06 | -0.08 | -0.10 | -0.12 | -0.14 | -0.16 | -0.17 | -0.18 |
| 1000 | -0.19 | -0.20 | -0.21 | -0.22 | -0.23 | -0.24 | -0.25 | -0.25 | -0.26 | -0.26 |
| t90/ºC | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
| 1000 | -0.26 | -0.30 | -0.35 | -0.39 | -0.44 | -0.49 | -0.54 | -0.60 | -0.66 | |
| 2000 | -0.72 | -0.79 | -0.85 | -0.93 | -1.00 | -1.07 | -1.15 | -1.24 | -1.32 | -1.41 |
| 3000 | -1.50 | -1.59 | -1.69 | -1.78 | -1.89 | -1.99 | -2.10 | -2.21 | -2.32 | -2.43 |
* A discontinuity in the first derivative of (t90 - t68) occurs at a temperature of t90 = 630.6 ºC, at which (t90 - t68) = - 0.125 ºC


